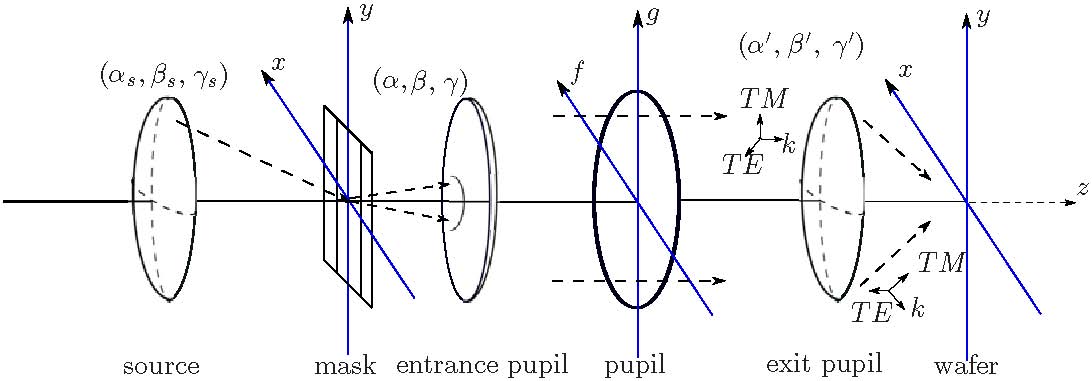
The gradient flow of the \(\mathcal{E}\left({\Phi }\right)\) is
\(\frac{\partial {\Phi }}{\partial \mathrm{t}}=-\mathrm{\mu }\frac{\partial {\mathcal{R}}_{\mathcal{P}}}{\partial {\Phi }}-\frac{\partial {\mathcal{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}}{\partial {\Phi }},\mathrm{ }\) (10)
where the Gâteaux derivative of \({\mathcal{R}}_{\mathcal{P}}\) in Equation (13) is given as [26]
\(\frac{\partial {\mathcal{R}}_{\mathcal{P}}}{\partial {\Phi }}=-\nabla \bullet \left({d}_{\mathcal{P}}\left(\left|\nabla {\Phi }\right|\right)\nabla {\Phi }\right),\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\) (11)
and \({d}_{\mathcal{P}}\) defined as
\({d}_{\mathcal{P}}\left(\left|\nabla {\Phi }\right|\right)=\frac{{\mathcal{P}}^{\mathrm{\text{'}}}\left(\left|\nabla {\Phi }\right|\right)}{\left|\nabla {\Phi }\right|}\) . (12)
Combining with Equation (6), the variational formulation in Equation (13) can be further expressed as
\(\frac{\partial{\Phi }}{\partial \mathrm{t}}=\mathrm{\mu }\left[∆{\Phi }-\nabla \bullet \left(\frac{\nabla{\Phi }}{\left|\nabla{\Phi }\right|}\right)\right]-\frac{\partial {\mathcal{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}}{\partial {\Phi }},\) (13)
with \(∆\) being the Laplacian operation.
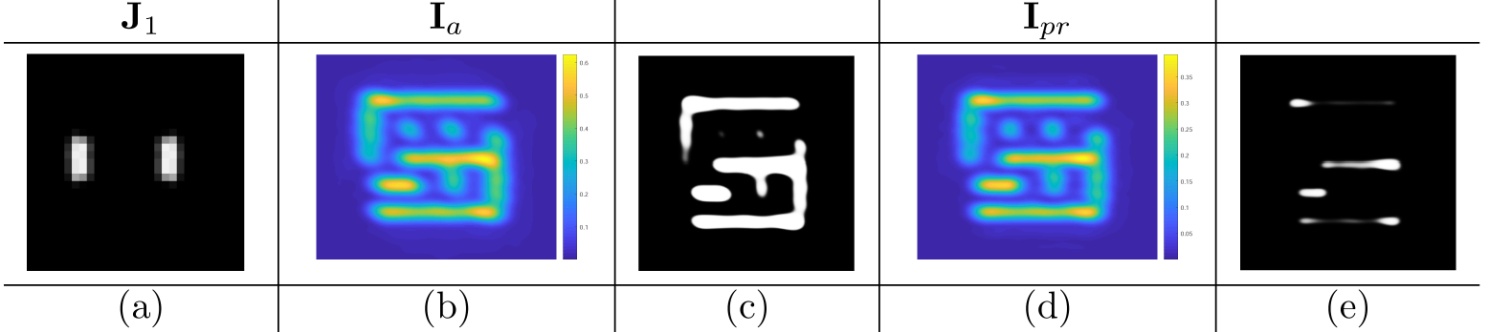
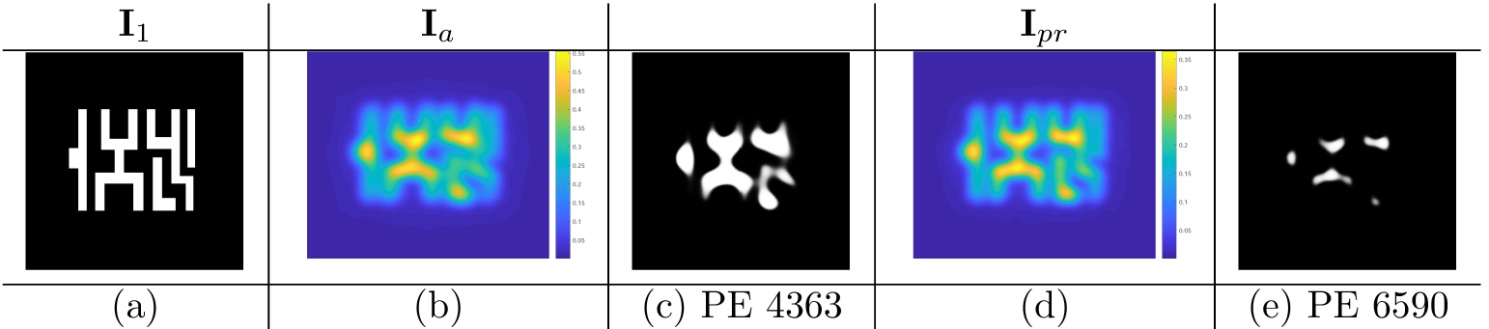
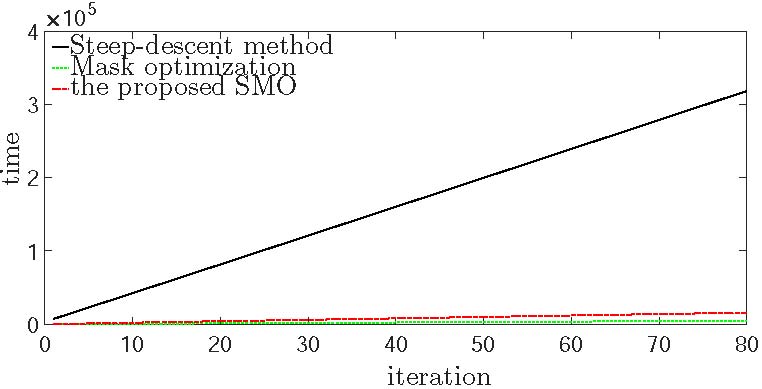
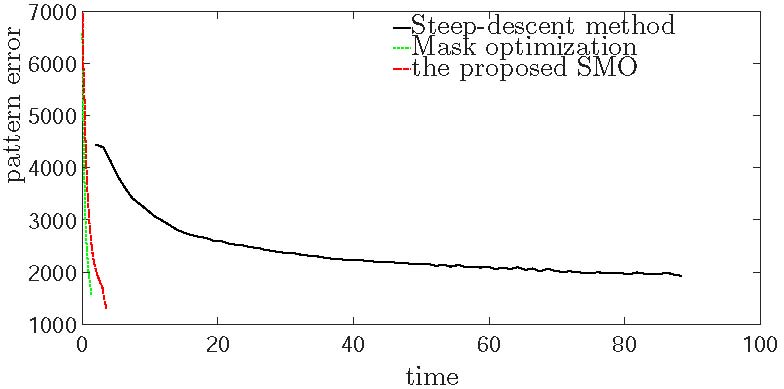
From Reference [25], it is noted that the edge placement error (EPE) has a positive relationship with the pattern error which is the sum of the mismatches between the printed image and the desired one over all locations in general. However, explicit incorporation of the EPE into the cost functions is often too complicated. Therefore, in this paper the distance metric \(\mathrm{d}\left\{\bullet ,\bullet \right\}\) in Equation (1) is defined as the pattern error (PE) to show the validity of the proposed variational level-set based SMO method. However, other distance metrics including EPE, process variation (PV) band and their combinations could be incorporated into the cost functions. Minimizing the external energy term \({\mathcal{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\) relates to solving Equation (1) with a least squares seeking the minimizer of
\(\mathrm{F}\left(\mathbf{J},\mathrm{ }\mathbf{M}\right)=\frac{1}{2}{‖\mathcal{T}\left\{\mathbf{J},\mathrm{ }\mathbf{M}\right\}-{\mathbf{I}}_{0}‖}^{2},\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\) (14)
where \(‖\bullet ‖\) stands for the \({\mathcal{l}}_{2}\) norm. The source and mask co-optimization approach updates both \(\mathbf{J}\) and \(\mathbf{M}\) in each iteration, which is explicitly revealed by the evolution of level surfaces represented by the time-dependent models with respect to and \({\Phi }\), namely,
\(\frac{\partial {{\Phi }}_{\mathbf{i}}}{\partial \mathrm{t}}=-\left|\nabla {{\Phi }}_{\mathbf{i}}\right|{\mathcal{v}}_{\mathbf{i}}\left(\mathbf{r},\mathrm{ }\mathrm{t}\right),\mathrm{ }\mathbf{i}=\mathbf{J}\mathrm{ }\ \mathrm{o}\mathrm{r}\ \mathrm{ }\mathbf{M},\) (15)
In which \({\mathcal{v}}_{\mathrm{J}}\left(\mathbf{r},\mathrm{ }\mathrm{t}\right)\) and \({\mathcal{v}}_{\mathbf{M}}\left(\mathbf{r},\mathrm{ }\mathrm{t}\right)\) are the velocity functions normal to the surfaces of \({\Phi }_{\mathbf{J}}\) and \({\Phi }_{\mathbf{M}}\), respectively, and are defined as
\({\mathcal{v}}_{\mathrm{J}}\left(\mathbf{r},\mathrm{ }\mathrm{t}\right)=-{\mathcal{J}\left\{\mathbf{J}\right\}}^{\mathrm{T}}\left(\mathcal{T}\left\{\mathbf{J}\right\}-{\mathbf{I}}_{0}\right)=\frac{1}{2}\frac{\mathrm{\vartheta }}{\mathrm{\vartheta }\mathbf{J}}{\left(\mathbf{I}-{\mathbf{I}}_{0}\right)}^{2}=2\mathrm{a}\sum _{{\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}}\frac{\sum _{\mathrm{p}=\mathrm{x},\mathrm{y},\mathrm{z}}{‖{\mathbf{E}}_{\mathrm{p}}\left({\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}\right)‖}^{2}-{\mathbf{I}}_{\mathrm{a}}}{\sum _{{\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}}\mathbf{J}}⨀\left({\mathbf{I}}_{0}-\mathbf{I}\right)⨀\mathbf{I}⨀\left(1-\mathbf{I}\right)\) , (16)
and
\({\mathcal{v}}_{\mathrm{M}}\left(\mathbf{r},\mathrm{ }\mathrm{t}\right)=-{\mathcal{J}\left\{\mathbf{M}\right\}}^{\mathrm{T}}\left(\mathcal{T}\left\{\mathbf{M}\right\}-{\mathbf{I}}_{0}\right)=\frac{1}{2}\frac{\mathrm{\vartheta }}{\mathrm{\vartheta }\mathbf{M}}{\left(\mathbf{I}-{\mathbf{I}}_{0}\right)}^{2}=-\frac{2\mathrm{a}}{\sum _{{\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}}\mathbf{J}}\sum _{{\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}}\sum _{\mathrm{p}=\mathrm{x},\mathrm{y},\mathrm{z}}\mathbf{J}\left({\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}\right)\)\(\mathrm{R}\mathrm{e}\mathrm{a}\mathrm{l}\left[{\left(\mathbf{B}\right)}^{\mathrm{*}}⨀\left({\left({\mathbf{H}}_{\mathrm{p}}^{\mathrm{*}}\right)}^{\diamond }\left\{{\mathbf{E}}_{\mathrm{p}}\left({\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}\right)⨀\left({\mathbf{I}}_{0}-\mathbf{I}\right)⨀\mathbf{I}⨀\left(1-\mathbf{I}\right)\right\}\right)\right]\mathrm{ }\) , (17)
with \(\mathcal{J}\left\{\bullet \right\}\) being the Jacobian, \(\mathrm{*}\) being the conjugate operation, \(\diamond \) flipping the matrix in the argument in both up-down and right-left directions, \(1\in {\mathcal{R}}^{\mathrm{N}×\mathrm{N}}\) being the all-ones matrix and \({\mathbf{E}}_{\mathrm{p}}\left({\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}\right)={\mathbf{H}}_{\mathrm{p}}\left({\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}\right)\otimes \mathbf{B}\left({\mathrm{\alpha }}_{\mathrm{s}},{\mathrm{\beta }}_{\mathrm{s}}\right)⨀\mathbf{M}\). Putting back into Equation (16) yields
\(\frac{\partial {{\Phi }}_{\mathbf{i}}}{\partial \mathrm{t}}=\mathrm{\mu }\left|\nabla {{\Phi }}_{\mathbf{i}}\right|\left[∆{{\Phi }}_{\mathbf{i}}-\nabla \bullet \left(\frac{\nabla {{\Phi }}_{\mathbf{i}}}{\left|\nabla {{\Phi }}_{\mathbf{i}}\right|}\right)\right]-\left|\nabla {{\Phi }}_{\mathbf{i}}\right|{\mathcal{v}}_{\mathbf{i}}\left(\mathbf{r},\mathrm{ }\mathrm{t}\right)={-\left|\nabla {{\Phi }}_{\mathbf{i}}\right|\mathrm{g}}_{\mathbf{i}}\left(\mathbf{r},\mathrm{ }\mathrm{t}\right),\mathrm{ }\mathbf{i}=\mathbf{J}\ \mathrm{ }\mathrm{o}\mathrm{r}\ \mathrm{ }\mathbf{M},\) (18)
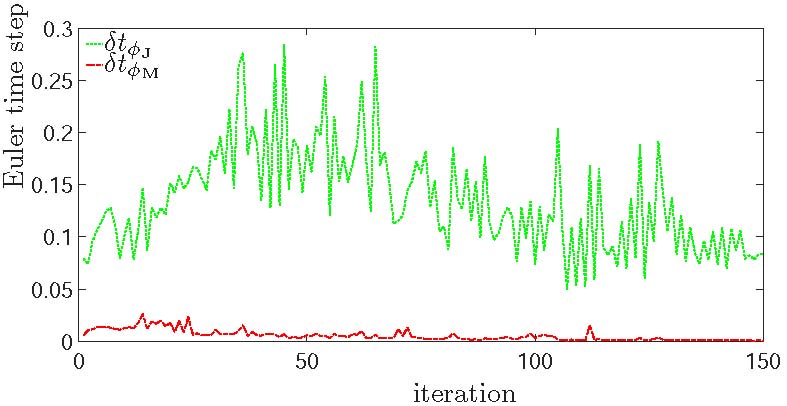
where \({\mathrm{g}}_{\mathbf{i}}\left(\mathbf{r},\mathrm{ }\mathrm{t}\right)=\mathrm{\mu }\left(∆{{\Phi }}_{\mathbf{i}}-{\mathcal{v}}_{\mathbf{i}}-\nabla \bullet \left(\frac{\nabla {{\Phi }}_{\mathbf{i}}}{\left|\nabla {{\Phi }}_{\mathbf{i}}\right|}\right)\right)\). In Equation (18), the gradient magnitude \(\left|\nabla {\Phi }\right|\) is multiplied to the right hand side of the equation, which accelerates the movement of the level curves of \({\Phi }\) and regularizes the parabolic term in a nonlinear way [21]. Generally, for convergence and stability, Courant-Friedrichs-Lewy (CFL) condition [33] is often applied asserting that the numerical wave speed must be at least as fast as the physical wave, giving
\(\mathrm{\delta }\mathrm{t}\bullet \mathrm{m}\mathrm{a}\mathrm{x}\left\{\frac{\left|{\mathrm{g}}_{\mathrm{x}}\right|}{\mathrm{\delta }\mathrm{x}}+\frac{\left|{\mathrm{g}}_{\mathrm{y}}\right|}{\mathrm{\delta }\mathrm{y}}\right\}=\mathrm{\epsilon },\) (19)
where \(\mathrm{\delta }\mathrm{x}\) and \(\mathrm{\delta }\mathrm{y}\) are the grid size of the discrete Cartesian grid, \({\mathrm{g}}_{\mathrm{x}}\) and \({\mathrm{g}}_{\mathrm{y}}\) are the components of \(\mathrm{g}\) in the \(\mathrm{x}\) and \(\mathrm{y}\) direction, \(0<\mathrm{\epsilon }<1\mathrm{ }\)is the CFL number and\(\mathrm{\delta }\mathrm{t}\) is the Euler time step, which for numerically stability is evaluated in every iteration.