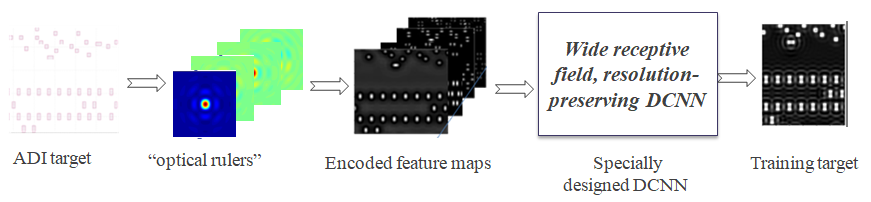
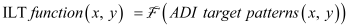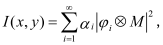Machine learning based ILT can be generally stated as: For a given ADI target layer and a fixed optimal mask generation mechanism (illumination source + mask type + rigorous ILT algorithm), there should exist a unique mapping function between ADI target data and ILT data, as shown in Figure 1.
Figure 1.
Mapping from ADI target to ILT image. Mathematically,it can be expressed as
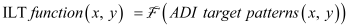
(1)
As we emphasized earlier, it is not a point-to-point mapping, it is a function-to-point mapping. The value of ILT solution at point (x, y) not only depends on the value of ADI target data at point (x, y), but also depends on all values of ADI target data around the point (x, y) within an influence range. Before we proceed to address the question of how to design feature vector to describe the neighboring environment around a point (x, y), we should first ask the question: how many degrees of freedom does the neighboring environment around a point (x, y) have? The theoretical answer is: the degree of freedom of the neighboring environment around a point (x, y) is infinite. Therefore, a complete description of the neighboring environment around a point (x, y) is impossible. Fortunately, a description with infinite resolution is often not required practically. This is true for machine learning based computational lithography, because the imaging system used in lithography process does not possess infinite resolution. This fact suggests that the number of effective degree of freedom of the neighboring environment around any point (x, y) can be considered finite practically. This observation and fact is the very foundation of all computational lithography. The second question we need to address is: what is a feature vector and what desired properties a feature vector should have? Essentially, a feature vector is a mathematical representation that describes the neighboring environment around a point (x, y) in a quantitative way. As a measurement device, a feature vector must address the following important properties, i.e., the measurement resolution, the measurement sufficiency (completeness), and the measurement efficiency. In addition, it is very desirable for a feature vector to possess a property such that the mapping function from input to output of the neural network model is less nonlinear and smooth (differentiable), or even monotonic (hopefully).
Figure 2.
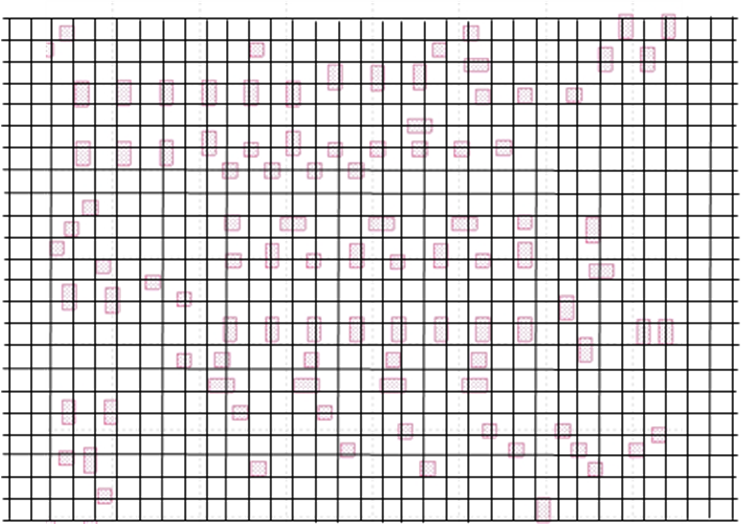
Divide the neighboring environment into cells. To elucidate the concept of measurement resolution and measurement efficiency of a feature vector, we can look at Figure 2. To describe the neighboring environment around a point (x, y), we can divide the influencing area into small cells. Assume the influencing range is 1.0 μm each side, and the cell size is x nm, then the cell size x determines the resolution of the feature vector representation, and the total number of cells = (2·1000/x)2 represents the maximum length of the feature vector for a complete description with resolution x nm. Clearly, the smaller the cell size x, the higher the measurement resolution; and the higher the resolution of the feature vector representation, the longer the feature vector is. To serve the machine learning based ILT properly, the resolution of the feature vector representation must meet a minimum requirement, which is determined by lithography process imaging condition, i.e., cell size x = k·λ/(NA(1+σmax)). The k coefficient is related to the degree of spatial coherence of the illumination, which depends on the effective illumination area of the source. A typical cell size for high NA immersion lithography process is around 15nm to 20nm, therefore, the estimated feature vector length for a complete description is (2000/20)2 = 10000. Of course, such a simple and plain encoding scheme for neighboring environment lacks of efficiency, because the encoding scheme does not explore the characteristics of the lithography process, it treats all cells equally and independently, it does not explore all symmetry properties among all the cells. Intuitively, not every cell has the same influence on the point of interest, on average, the closer the cell to the point of interest, the more important the cell is. As to the sufficiency of a feature vector, it is related to the capability of the feature vector in describing the neighboring environment completely within allowed error bound. Simply stated, for any two feature vectors X1 , X2 , if X1 = X2 , then, the condition |F (X1 ) - F (X2 )| ≤ ε (ε is the allowed error bound related to data noise) CANNOT be violated.
There have been several reported ways of designing feature vectors for computational lithography. Incremental concentric square sampling
[15], incremental concentric circle area sampling
[16], polar Fourier transform
[17] have all been proposed to be used for constructing feature vectors for computational lithography. These feature vector designs do not address the optimality of the designed feature vector, and most of them are pure geometrical based feature vectors, except the design based on polar Fourier transform. Feature vectors based on “
geometrical rulers” have intrinsic deficiency in machine learning computational lithography; this is particularly true for inverse lithography which grows assist features out of blank areas in mask space. As it is known, rule based assist feature insertion based on geometrical measurement has abrupt change points in the rule table. Therefore, machine learning inverse lithography using “geometrical ruler” based feature vector as neural network input must possess more complicated network structure to learn those abrupt change points in order to map the feature vector into correct response function domain. Feature vectors derived from polar Fourier transform made progress by exploring the characteristics of the lithography process partially, however, it still fails to fully take the imaging process physics into account. Feature vector design is essentially an information encoding scheme design. For machine learning computational lithography, there are three spaces we can use for information encoding, the lithography target space, which is pure geometrical; the mask space, which has geometrical information and optical property information; the image space, which contains information about design geometries, mask optical properties and imaging formation characteristics. From an information point of view, information in lithography target space is not complete (without specifying optical properties of the background and the pattern covered areas), if feature vector design is in lithography target space, then the subsequent DCNN must learn mask optical properties, nonlinear imaging formation process and rigorous ILT algorithm. Information in mask space is complete and of highest resolution. If feature vector design is in mask space, then the subsequent DCNN must learn nonlinear imaging formation process and rigorous ILT algorithm. Information in imaging space can be used to recover information in mask space fully within the resolution limit defined by optical imaging condition. If feature vector design is in image space, then the subsequent DCNN
only need to learn the rigorous ILT algorithm. Between mask space and image space, which space is narrower in terms of encoding efficiency? In mask space, the “function space” is constrained by design rules of the layer; while in image space, the “function space” is constrained by both design rules and imaging conditions. Stated explicitly,
all aerial images derived from a given imaging condition constitute a special class of functions. In other words, the “function space” in image space is narrower than the “function space” in mask space, and the information lost in image space in comparison with that in mask space is beyond the optical imaging resolution. Therefore, optimal feature vector design for computational lithography should be related to optimal and efficient representation of aerial images of the class at hand.
Now the question becomes how to represent aerial images most efficiently?The aerial image function I(x,y) is a band-limited function. While a real function with finite bandwidth Ω can always be represented by a set of basis functions of the same bandwidth, there still exists the question whether there is an optimum set of basis functions among all the possible sets of basis functions with bandwidth, Ω. By the optimum set of basis functions, it means that only the minimum number of the basis functions that are needed to approximate any real valued function of bandwidth, Ω, for a specified error requirement. To seek the optimal representation of aerial image function, we can refer to the imaging equation of Hopkin’s, which can be decomposed into a sum of coherent imaging system for partially coherent illumination, as shown in Equation (2) below.
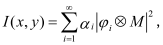
(2)
where ⊗ represents the convolution operation between the
ith kernel and the mask transmission function M. {
Φi} and {
αi} are the set of eigenfunctions and eigenvalues of the transmission cross coefficients matrix (TCCs). This optimal imaging system decomposition is originally designed for fast aerial image calculation under partial coherent illumination, and it has been proved that this decomposition scheme is the optimal decomposition in terms of computational efficiency
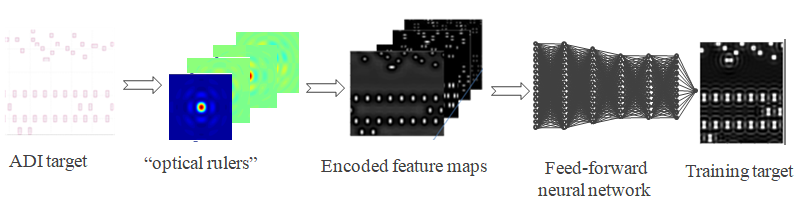
[18]. From an information theory point of view, we can interpret it as an optimal and most efficient aerial image information encoding scheme. This suggests that imaging system kernels {
Φi} captures imaging system characteristics fully, and they are a set of natural and optimal “
optical rulers” for measuring or estimating the neighboring environment around a point (
x,
y), because the set of {
Φi} eigenfunctions are orthonormal functions. Based on the above reasoning, we define {
S1 ,
S2 , … ,
SN } as the feature vector, with
Si being defined as

(3)
Then, the machine learning inverse lithography problem can be reformulated from Equation (1) to Equation (4).

(4)
The idea of using imaging eigen signal set {
Si } to describe aerial image has been used previously for OPC model and lithography two-dimensional patterns’ quantification
[19, 20]. Now we turn to the question of how to obtain the approximate function
F, this is related to neural network design.