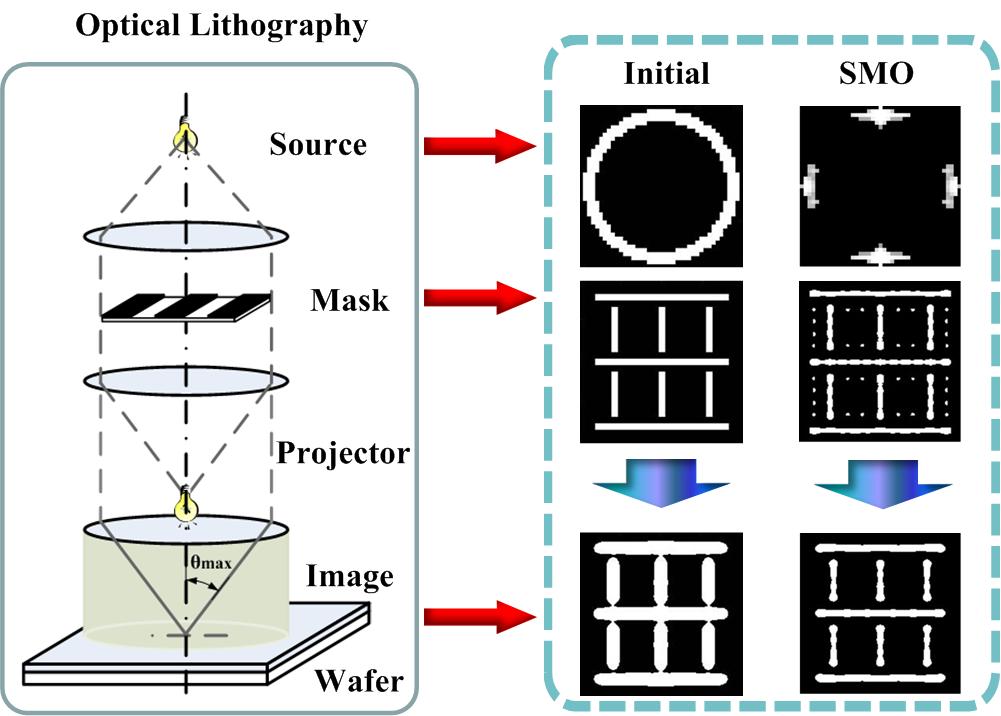
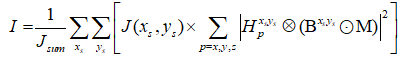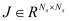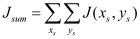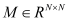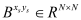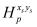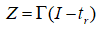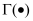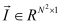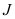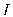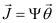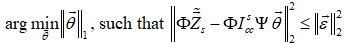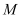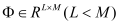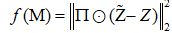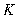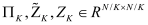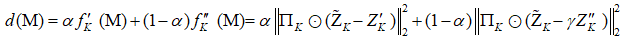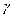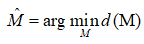This section provides simulation results of the proposed CS-SMO method, and compares it to the traditional gradient-based SMO algorithm. In the following simulations, we use an immersion lithography system with 1.2 numerical aperture and a four-fold demagnification factor for the projection optics.
Figure 2 illustrates the simulations based on a dense line-space layout pattern with CD = 45nm. The first row illustrates the simulation using the initial source pattern and initial mask pattern. The second row shows the result obtained by the traditional gradient-based SMO algorithm proposed in Reference [9]. In the traditional hybrid SMO algorithm [9], the source pattern is firstly individually optimized, and then the mask pattern is individually optimized. Finally, the source and mask patterns are simultaneously optimized for several times. The third row illustrates the simulation of the proposed CS-SMO algorithm. From left to right, it respectively shows the source patterns, mask patterns, and the print images on the focal plane and defocus plane. The values of pattern error (PE), edge placement error (EPE), normalized image log slop (NILS) and aerial image contrast are used as the metrics to assess the lithography imaging performance. The NILS and aerial image contrast are measured along the red dotted line in the figures. In this simulation, the SO problem is solved by the LB algorithm. The runtime of the traditional gradient-based SMO algorithm is about 214,695s. On the other hand, the runtime of the proposed CS-SMO algorithm is about 39,945s. It is noted that the runtime should be changed with the computational resources used and the scale of the layout patterns. It is observed that proposed CS-SMO algorithm will results in better imaging performance than the traditional gradient-based SMO algorithm, and speed up the computational efficiency by 81% as well.
Figure 2.
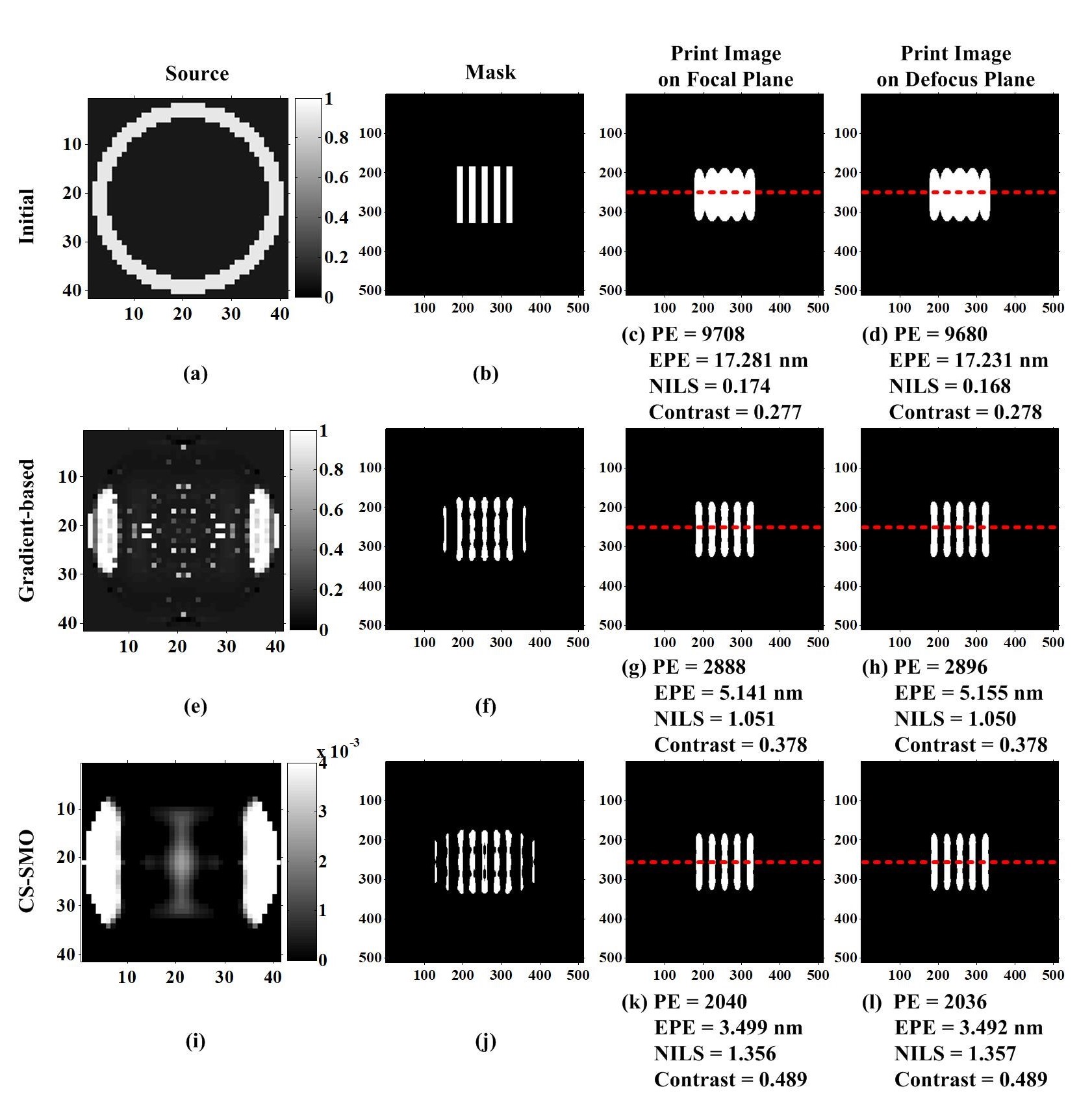
Comparison of CS-SMO and gradient-based SMO algorithms using a vertical line-space pattern. Figure 3 uses another horizontal block pattern to run the simulations of the CS-SMO and gradient-based SMO algorithms. In this simulation, the SO problem is solved by the LB algorithm. The runtimes of the traditional gradient-based SMO algorithm and the proposed CS-SMO algorithm are 214,485s and 25,243s, respectively. The simulation results in Figure 3 also proves the superiority of the proposed CS-SMO algorithm over the traditional gradient-based SMO algorithm in terms of the imaging performance and the computational efficiency.
Figure 3.
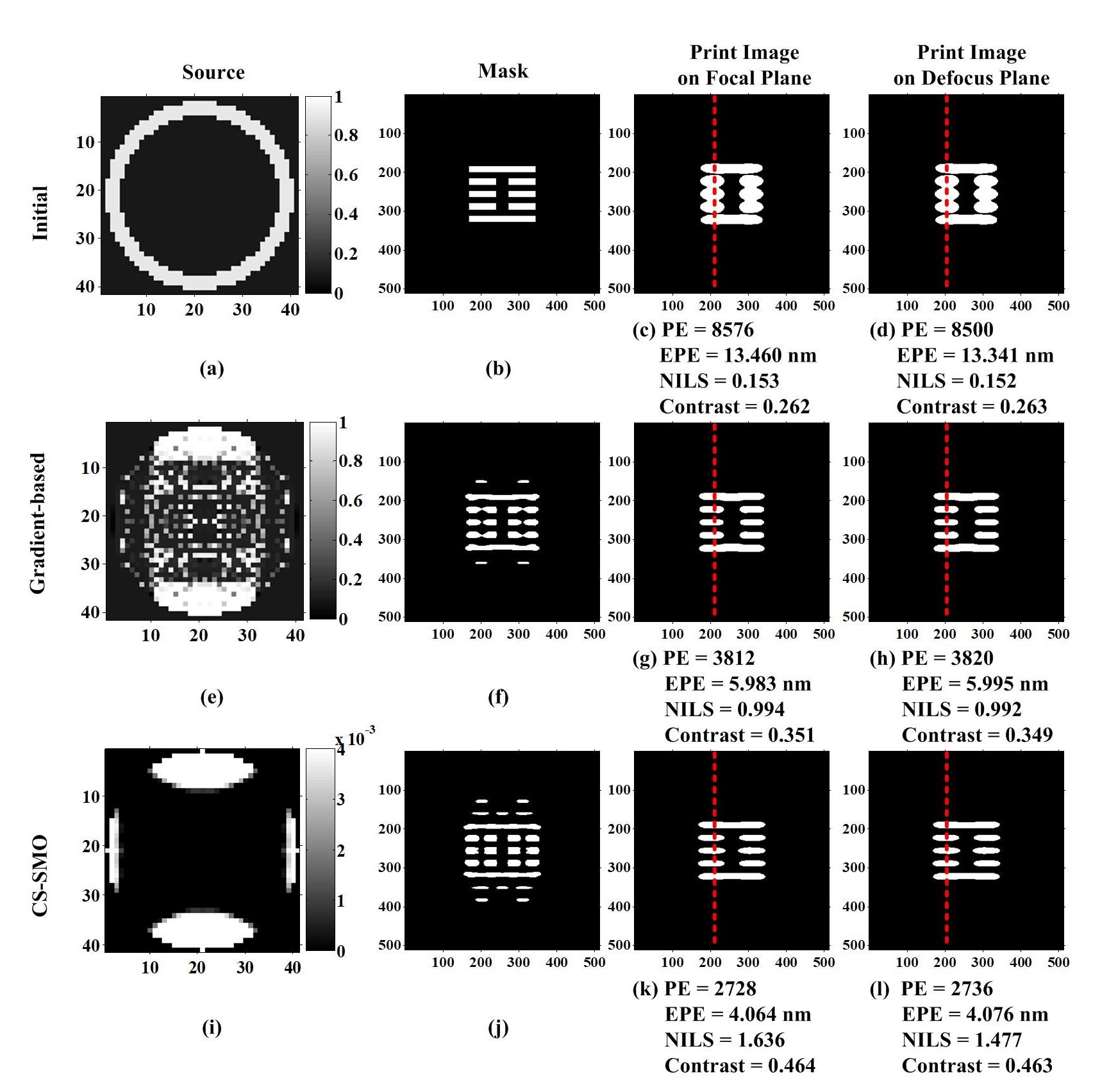
Comparison of CS-SMO and gradient-based SMO algorithms using a horizontal block pattern. In Figure 4, we assess the proposed CS-SMO method based on a complex layout pattern. The first row shows the simulation of the traditional gradient-based SMO algorithm. The second row shows the simulation of the proposed CS-SMO algorithm, where the GPRS algorithm is used to solve for the SO problem, and the MO problem is still solved by the IHT algorithm. The NILS and aerial image contrast are measured along the red dotted line in the figures. The runtimes of the traditional gradient-based SMO algorithm and the proposed CS-SMO algorithm are about 214,610s and 13,143s, respectively. Compared to the traditional gradient-based SMO algorithm, the CS-SMO algorithm is more efficient, and achieves higher image fidelity of the lithography system.
Figure 4.
Comparison of CS-SMO and gradient-based SMO algorithms using a complex layout pattern.